The Difficulty of Kissing

Posted on by Tamás Görbe

The kissing number problem belongs to the realm of geometry. It’s intimately connected to sphere packing, lattices and spherical codes as well as various other branches of mathematics, such as group theory, Lie theory, optimization theory and the list goes on [1]. In this short post, I’ll describe the problem itself with a bit of its interesting history and say a few words about the known solutions.

So what is the kissing number problem? The task sounds fairly simple. Take a unit ball in {n} dimensions and put as many unit balls in contact with it as you can in such a way that the surrounding spheres do not overlap. What’s the maximal number of touching unit spheres? This number is the {n}-dimensional kissing number, which we denote by {K_n}.

One-dimensional balls are just intervals and a given interval can only be in contact with two intervals so it is clear that {K_1=2}.

The kissing number in 1D is two.
The kissing number in 1D is two.

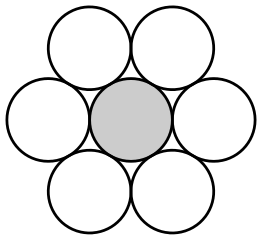
In two dimensions, if two unit disks {D_1,D_2} touch the given one {D}, their centres {C_1,C_2,C} form a triangle with sides of length {|CC_1|=|CC_2|=2} and {|C_1C_2|=4\sin(\alpha/2)}, where {\alpha} is the angle at {C}. The overlap condition on {D_1,D_2} implies that {\alpha\in[\frac{\pi}{3},\pi]}, thus the minimal length of third side is {2}, which happens at {\alpha=\frac{\pi}{3}}, i.e. when {CC_1C_2} forms an equilateral triangle. This shows that six such disks can be arranged around {D} with no space left between them yielding {K_2=6}.

The kissing number in 2D is six.
The kissing number in 2D is six.

The kissing number in three dimensions was the subject of a famous correspondence between Isaac Newton and David Gregory in 1694. Newton correctly thought that the kissing number was twelve, as found in the fcc lattice, but Gregory thought that a thirteenth sphere could fit. That’s why the {n=3} case is often referred to as the problem of thirteen spheres. One would think that this debate should be easily resolved, but a rigorous mathematical proof was lacking until 1953, when Schütte and van der Waerden [2] gave a detailed argument proving that {K_3=12}. An elementary proof was given by Leech in 1956 [3], but his proof is still far from being trivial. There has been effort to bring Leech’ proof down the level of an elementary undergraduate course [4].

We mention as an interesting fact, that although Gregory was wrong about the thirteenth sphere, there is still a lot of space left between the spheres after the kissing number is reached. In fact, there is enough room for the balls that any permutation of them can be achieved by moving them continuously on the surface of the middle sphere, while staying in touch with it. There is a nice constructive proof of this, which uses the fact that {K_3} is realized by the icosahedron, as depicted below. For details, see [1] pp. 29-30.

The kissing number in 3D is twelve.
The kissing number in 3D is twelve.

The {3}-dimensional case already demonstrates that the kissing number problem is highly non-trivial and things become even more difficult in higher dimensions. No general formula is known for {K_n}.

The solution for four dimensions was given by Oleg Musin in 2003 [5]. He proved that {K_4=24} as realized by the 24-cell. For {n=5,6,7} the kissing number is not known, only lower and upper bound are shown. Somewhat surprisingly, the eight- and twenty-four-dimensional kissing numbers are proved to be {K_8=240} and {K_{24}=196,560}. Both was proved by Odlyzko/Sloane [6] and Levenshtein [7] independently in 1979. These special dimensions (8 and 24) seem so random at a first glance, but in fact they’re not a coincidence. Their exceptional nature is explained by the existence of some highly symmetric objects. The former case is realized by the {E_8} root system, which I’ve previously mentioned here and here. {K_{24}} is realized by the Leech lattice. As for the bounds, Bachoc and Vallentin [8] developed a method, based on semidefinite programming, to find upper bounds for the kissing number. This was used in high accuracy calculations [9] to produce upper bounds on the kissing number in {n}-dimensions for {n\leq 24}. 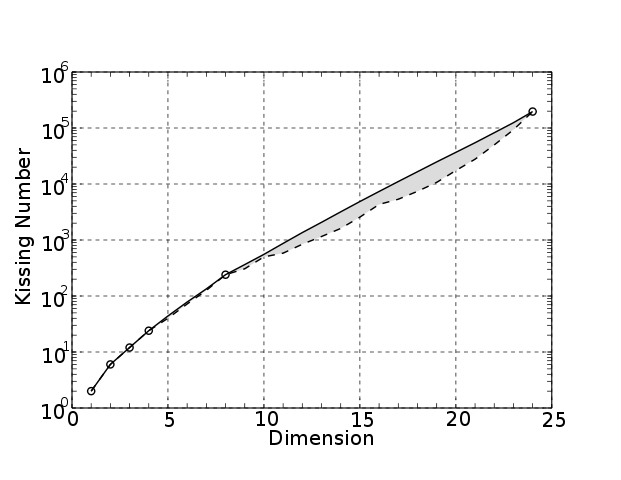The table below contains bounds (found in [10]) which might not be up-to-date.

Dimension Lower bound on {K_n} Upper bound on {K_n}
1 2
2 6
3 12
4 24
5 40 45
6 72 78
7 126 134
8 240
9 306 364
10 500 554
11 582 870
12 840 1357
13 1154 2069
14 1606 3183
15 2564 4866
16 4320 7355
17 5346 11,072
18 7398 16,572
19 10,668 24,812
20 17,400 36,764
21 27,720 54,584
22 49,896 82,340
23 93,150 124,416
24 196,560

Table. Bounds on kissing numbers in {n}-dimensions for {n\leq 24}. (Known kissing numbers are in boldface.)

These numbers suggest an exponential growth of {K_n} and indeed it has been shown that

\displaystyle 2^{0.2075n(1+o(1))}\leq K_n\leq 2^{0.401n(1+o(1))}.

Bounds on kissing numbers in n-dimensions for n less then 25.
Bounds on kissing numbers in {n}-dimensions for {n\leq 24}.
  1. J.H. Conway, N.J.A. Sloane, Sphere packings, lattices and groups, 3rd edition, Springer, 1999.
  2. K. Schütte, B.L. van der Waerden, Das problem der dreizehn kugeln, Math. Ann. 125, 325-334 (1953)
  3. J. Leech, The problem of thirteen spheres, Math. Gaz. 40, 22-23 (1956)
  4. H. Maehara, The problem of thirteen spheres – a proof for undergraduates, European J. Combin. 28, 1770-1778 (2007)
  5. O.R. Musin, The kissing number in four dimensions, Ann. of Math. 168, 1-32 (2008)
  6. A.M. Odlyzko, N.J.A. Sloane, New bounds on the number of unit spheres that can touch a unit sphere in n dimensions, J. Combin. Theory Ser. A 26, 210-214 (1979)
  7. V.I. Levenshtein, On bounds for packing in n-dimensional Euclidean space, Soviet Math. Dokl. 20, 417-421 (1979)
  8. C. Bachoc, F. Vallentin, New upper bounds for kissing numbers from semidefinite programming, J. Amer. Math. Soc. 21, 909-924 (2008)
  9. H.D. Mittelmann, F. Vallentin, High-accuracy semidefinite programming bounds for kissing numbers, Experiment. Math. 19, 174-178 (2010) 
  10. P. Boyvalenkov, S. Dodunekov, O.R. Musin, A survey on the kissing numbers, Serdica Math. J. 38, 507-522 (2012)

Leave a comment